前言

近十年来，互联网领域出现了相当多的名词概念，如 Web3、元宇宙等。这些新产生的概念大多数并没有一个相对权威的、精准的定义，与其称它们为新的技术概念，倒不如用“愿景”一词来描述它们显得更为准确。以 Web3 为例，在各式各样的定义当中，所表达出来的实际上是一种对去中心化网络的期望。

用户的个人信息、生产的内容、所能获取得到的信息不再依托于某个中心平台进行存储、分发、授权，每一个人都自由地相互交换信息，没有任何一个垄断平台有权力阻断这个过程。很显然，这损害了当下几乎所有平台内容提供商的利益，相关技术的推广也必然受到巨大的阻力。大概这也正是为何迄今为止，关于去中心化网络技术的相关概念仍只停留在愿景之中。

当我们尝试去构建一个去中心化的应用网络时，往往就会接触到区块链技术。由于区块链常与虚拟货币一起进入大众的视线，而虚拟货币又是一个极具争议的金融工具，因而导致区块链常常难以被作为一种技术进行讨论。在我看来，与元宇宙这种过于遥远显得有些骗局的概念相比，区块链作为一种去中心化的数据库技术，且在当前已拥有具体的实现并投入应用的状况下，要显得更为踏实可靠，也值得我们进行技术研究。

在下文中，我们将聚焦于讨论区块链作为数据库技术的实现与应用，尽可能地避免涉及虚拟货币——尽管它是当前区块链技术最大的应用。事实上，中央认为区块链技术的集成应用在新的技术革新和产业变革中起着重要作用，但炒作虚拟货币却是一种被中国政府所禁止的行为。这背后有相当复杂的金融与政治问题考量，与本文希望探讨的区块链技术本身相去甚远。

作为一种数据库技术，首先需要考察存储在其中的数据安全性如何得到保证，这将涉及相关加密算法的介绍与对比，并对其原理做出一定的实验与研究。其次，我们将简略考察区块链技术整体的架构组成，分析各层的作用及其之间的交互关系，并以数据结构的角度分析单一区块的结构组成，以研究位于区块链最底层数据层的工作方式。最后，我们将介绍一些区块链技术的实际应用。

目录

• 加密算法
  • 对称加密算法
  • 非对称加密算法
    • RSA 算法
    • ECC 算法
  • 密钥强度
    • 对称加密算法
    • 非对称加密算法
• 区块链
  • Merkle Tree
  • 区块数据结构
  • 共识机制
  • 与分布式数据库的区别
• 实际应用
  • 基于区块链的个人博客 - xLog
  • 基于区块链的云存储 - IPFS
• 结语

加密算法

在密码学中，加密是对信息进行编码的过程。这个过程将信息的原始表示形式（称为明文）转换为另一种替代形式（称为密文），在理想情况下，只有授权方才能将密文解密回明文并访问原始信息。加密算法描述了将明文编码为密文的具体操作方式，这一过程可被编写为一段程序进行执行。

与之相区别的另一种算法称为消息摘要算法，又称为散列算法或哈希函数，广泛用于消息签名、文件完整性校验等应用，如 MD5、SHA、MAC 等。这一类算法将消息或数据压缩成摘要，不同的数据所得到的摘要信息也不相同，无法通过逆向获得原始信息，因此也不能被称为加密算法。

在人类社会发展的早期，人们通过使用仅授权方所知的特定加密算法来完成信息加密，如凯撒密码。在信息交流不便的当时，加密算法能够较好的保持机密性。然而，当加密算法本身泄露后，原有的密文可能便立即得到破解，未授权方也能够使用这一加密算法创建新的密文信息，使得原加密工作失去意义。因此，随着信息交流越发便捷，现代密码学总是假定加密算法本身是公开的，一个安全的加密算法能够在这一前提下，使得未授权者无法、或者成本极其高昂地将一个密文解密回明文。

对称加密算法

为了实现这样的特性，一种很容易想到方案便是引入一种授权方内互相可知的密码。同一明文使用同一加密算法、不同的密码将编码得到不同的密文；使用同一算法、与加密时相同的密码进行解密，才能得到原始明文。这样，就从最初的保密加密算法转化为了保密密码。这种加密算法类型就是对称加密，所使用的密码被称为对称加密密钥。

常见的对称加密算法有 AES、ChaCha20、DES 等。由于对称加密算法在计算速度上要远优于非对称加密算法，因此当下有相当多的使用场景正在使用对称加密，如具备一定的抵抗中间人攻击能力的隧道代理协议 Shadowsocks。

非对称加密算法

在对称加密算法中，加解密过程所使用的密钥是相同的，即加密密钥同时也是解密密钥。尽管我们将保密加密算法转化为了保密密钥的工作，但却仍然面临着一方的密钥泄露将导致整条加密信道被破解的风险。是否存在那么一种加密算法，使得加密方所使用的密钥完全公开，而只要解密方所使用的密钥仍然保密，这条加密信道就仍是安全的呢？当然存在，这种加密算法类型就是非对称加密，加密方所使用的密钥被称为公钥，而解密方所使用的密钥被称为私钥。

常见的非对称加密算法有 RSA、ECC 等。这两种算法也广泛应用于区块链技术中，用于生成代表用户身份的签名信息。除此之外，TLS 技术也基于非对称加密算法实现，形成了一整套证书信任机制，驱动着当代互联网举足轻重的 HTTPS 协议。

RSA 算法

RSA 是最有影响力的非对称加密算法之一，由 Ron Rivest、Adi Shamir 和 Leonard Adleman 提出。由于对大整数进行因式分解极其困难，因此选取两个大质数，其乘积可以作为加密密钥发布（即公钥），两个大质数的组合可以设置为私钥。从密文和公钥中取回明文消息的难度取决于分解两个大素数的乘积的难度。算法 $1$ 和 $2$ 分别表示 RSA 加密和解密的算法。

算法 $1$：RSA 加密

输入： RSA 公钥 $(n, e)$，明文 $m \in [0, n - 1]$

输出： 密文 $c$

开始

1. 计算 $c = m^e \mod n$
2. 返回 $c$

结束

算法 $2$：RSA 解密

输入： 公钥 $(n, e)$，私钥 $d$，密文 $c$

输出： 明文 $m$

开始

1. 计算 $c = c^d \mod n$
2. 返回 $m$

结束

ECC 算法

1985 年，Neal Koblitz 和 Victor Miller 使用椭圆曲线实现了称为 Elliptic Curve Cryptography 的密码算法。ECC 是一种非对称加密算法，其中每个用户或设备都有一对密钥，一个公钥和一个私钥。ECC 的数学运算在椭圆曲线 $y^2 = x^3 + ax + b$ 上定义，其中 $4a^3 + 27b^2 6 \neq 0$，$a$ 和 $b$ 的每个值给出不同的椭圆曲线。公钥是曲线上的一个点，私钥则是一个随机数。公钥是通过将私钥与曲线中的生成点 $G$ 相乘来创建的。生成点 $G$、曲线参数 $a$ 和 $b$ 以及其他一些常量构成了 ECC 的域参数。算法 $3$ 和 $4$ 分别表示 ECC 中加密和解密的算法。

算法 $3$：ECC 加密

输入： 椭圆曲线的参数字段 $(p, E, P, n)$，公钥 $Q$，明文 $m$

输出： 密文 $(C1, C2)$

开始

1. 将明文 $m$ 表示为 $E(F_p)$ 中的点 $M$
2. 选择 $k \in R^{[1, n - 1]}$
3. 计算 $C1 = K_p$
4. 计算 $C2 = M + kQ$
5. 返回 $(C1, C2)$

结束

算法 $4$：ECC 解密

输入： 椭圆曲线的参数字段 $(p, E, P, n)$，私钥 $d$，密文 $(C1, C2)$

输出： 明文 $m$

开始

1. 计算 $M = C2 - dC1$，且 $m$ 来自 $M$
2. 返回 $m$

结束

密钥强度

衡量加密算法安全性的一个关键指标是密钥强度，密钥强度为 $k$ 意味着破解密钥的计算复杂度为 $2^k$，强度为 $128$ 代表目前最好的攻击算法需要计算 $2^{128}$ 才能攻破。下表列出了部分加密算法密钥强度。

对称加密

算法	密钥长度	密钥强度
DES	56
3DES-2	112	80 ~ 112
3DES-3	168	112
AES-128	128	128
AES-192	192	192
AES-256	256	256

非对称加密

ECC 算法密钥长度	RSA 算法密钥长度	密钥强度
112	512	56
160	1024	80
224	2048	112
256	3072	128
384	7680	192
512	15360	256

由表格可见，被以太坊与比特币所使用的 ECC 加密算法相比于 RSA 算法而言，可以使用更短的密钥长度得到相同的密钥强度。除此之外，ECC 在计算性能上也更优于 RSA 算法，其计算速度对比情况如下表所示。

ECC 密钥长度	RSA 密钥长度	ECC 计算时间(s)	RSA 计算时间(s)
163	1024	0.08	0.16
233	2240	0.18	7.74
283	3072	0.27	9.80
409	7680	0.64	113.90
571	15360	1.44	679.06

区块链

想象一个这样宏观的数据库，它所存储的数据分散在世界各地，每一台计算机都仅拥有其中的一部分数据。由于存储在某些计算机上的部分数据可能遭到损坏而不完整，因此每一个分散的数据的并集至少能够包含这个宏观数据库的所有数据。这些分散在世界各地的计算机就是该宏观数据库的存储与算力来源。

对于其中的单个节点而言，为了确保自身从这样一个宏观数据库中所取得的数据是正确且未被篡改的，它不能轻易信任来自其他节点的任何数据，因此，区块链需要一种机制来校验从其他节点下载而来的数据信息。另一方面，每个节点存储的都是来自世界各地用户的私人信息，如何确保单个节点无法读取这些隐私也是区块链需要解决的问题之一。区块链单一区块的数据结构设计能够很好的解决以上两个问题。

去中心化的宏观数据库不应受到任何独立个体的肆意控制，这意味着区块链需要有一种机制来确保任何人无法随意修改和删除已在链上的区块信息，至少修改成本应当相当高昂而不可接受。因此，这一机制将能够决定整个网络的所有节点中，由谁来创建新的区块并加入区块链。这一过程需要由各个节点达成一定的共识，因而于区块链的共识层中进行解决。

存储和算力毕竟是节点所拥有的资源，在一个互不信任的网络中，如何说服每个节点愿意主动出让自身所拥有的资源来构建这样一个宏观的数据库，也是区块链需要解决的问题之一。应当说，至少存在一种激励机制使得每个节点认为其有利可图，从而愿意主动为区块链贡献存储和算力资源，这一过程由激励层算法进行实现。

因此通常来说，区块链架构可被分为数据层、网络层、共识层、激励层、合约层和应用层。这不是绝对的，在一些区块链的设计中，可能并不存在激励层或激励机制，例如由区块链的发明者之一 Stuart Haber 在 $1995$ 年创建的最古老的区块链 Surety。

Merkle Tree

我们知道，消息摘要算法可以对文件进行数据摘要，得到一个独一无二的值。如果我们从一个中心服务器上下载文件，在完成下载后通过计算其哈希值，并与服务器所提供的哈希值进行比对，便可校验所下载的文件是否正确完整。如果文件不完整，则需要重新进行下载。

进一步地，如果将文件分割成一个个小的数据块，并对每个数据块计算哈希值，这些哈希值就构成了哈希列表。当我们使用 BitTorrent 协议从多台计算机中各自下载一部分文件数据块（或者使用多线程从中心服务器中下载文件）时，便可以相互独立地校验各个数据块的完整性。一旦部分文件数据不完整，则可仅下载该不完整的文件块而无需重新下载所有的文件。

如何确保哈希列表中的哈希值都是正确的呢？将它们拼接在一起所得的值再进行一次哈希，得到根哈希值，通过根哈希值便可确认哈希列表的完整性。而 BitTorrent 文件事实上也是如此设计的。

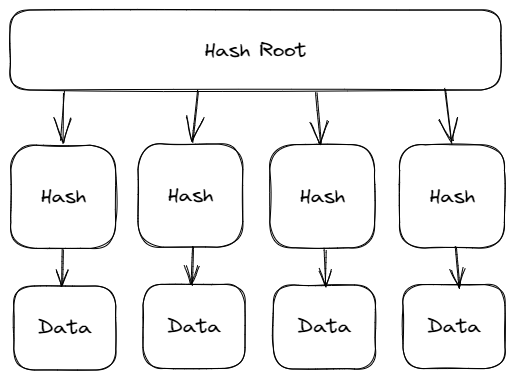
注意到我们的哈希列表已经形成了一个两层的树结构，如果更进一步，我们仍然将文件分成一个个小的数据块，每个数据块计算一次哈希值，每两个哈希值拼接在一起（单数文件块则无需拼接）进行一次新的哈希，成为其父节点，如此循环，最终可以构建得到一个具有单一根哈希值的二叉树。这棵二叉树便是Merkle Tree，即默克尔树，根哈希也被称为默克尔根。

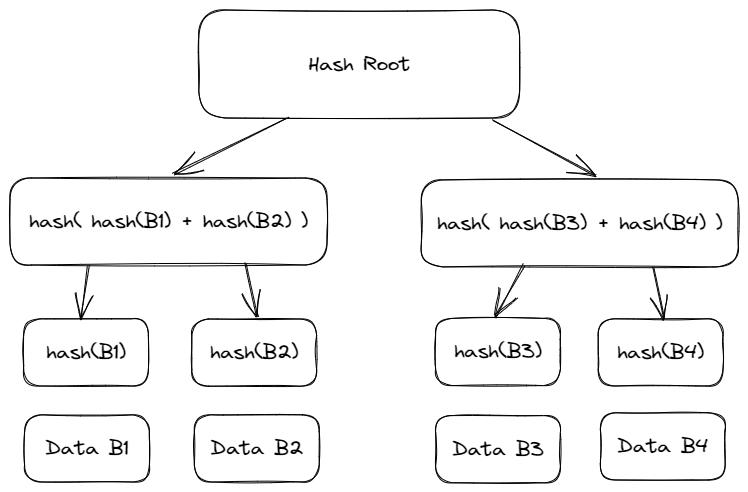
这样的数据结构具有这样的特点：单独取出其中的任何一棵子树（任何一段连续的文件数据块），都能够校验其完整性。

区块数据结构

区块链上的区块由区块头和区块体两部分组成。区块体存放区块所记录的数据信息，使用默克尔树数据结构进行存储，默克尔根则作为区块头的一部分信息进行存储。需要注意的是，区块体默克尔树中的叶子节点所存储数据并非明文信息，而是使用了非对称加密算法进行编码后的密文，仅数据所有者拥有私钥进行解密，这就保证了存储该数据的其他节点无法读取数据信息，确保了数据隐私。

区块头由版本号、前一区块的区块头哈希值、时间戳、默克尔根和实现共识机制的相关参数所组成。以使用 POW（工作量证明） 共识机制的比特币为例，其区块头含有随机数和目标哈希两个参数信息。整个区块头的哈希值即为该区块 ID，通过存储前一区块的 ID 值，各个区块得以链接形成区块链。区块链上任何一个区块总能向前追溯至根区块。

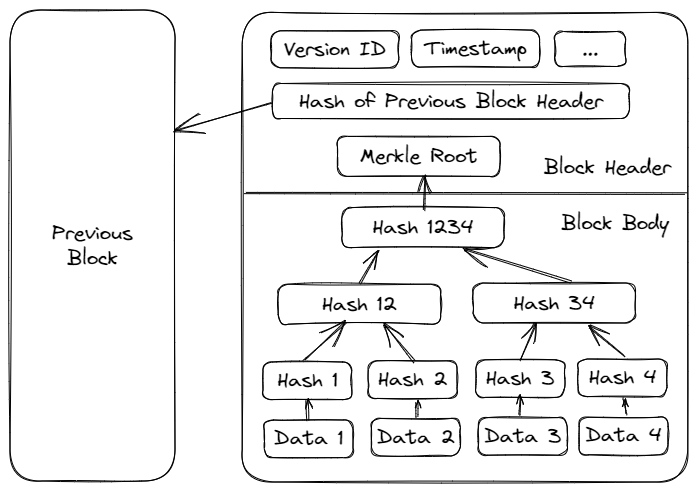
利用区块数据结构，各节点可以校验该区块的数据信息是否正确完整，向前追溯的特性则赋予了各节点检验该区块是否存在于区块链上的能力。但这仅能保证节点验证单一区块的正确与完整性，对于整个区块链的安全而言，还需要共识机制的运作来实现。

共识机制

在已经确保单个区块安全的背景下，如何实现区块链整体的不可篡改特性，是共识机制需要解决的问题。考虑这样一个场景，这个宏观数据库需要插入一条新的数据记录。在传统中心化数据库中，中心服务器的数据库引擎得到指令并完成了资源的创建和插入，而在以区块链为技术的宏观数据库中，该由谁来执行这一操作呢？

一个比较自然的想法是，网络中的各个节点进行投票，选出一个临时的超级管理员作为代表执行创建新区块、链接至区块链并通知其他节点进行同步的工作，这便是 DPOS（委托权益证明） 共识机制。除了这一共识机制外，还有其他的共识机制设计。例如，人们所熟知的比特币使用 POW（工作量证明） 共识机制，网络中的所有节点一同参与数学运算，谁先计算得到符合条件的结果，谁就拥有了记账权，并能获得一定的比特币作为担任“超级管理员”的报酬。

在区块数据结构本身与区块链共识机制的共同作用下，如果某个节点尝试篡改一个区块，则该区块的 ID 值必然发生改变（否则无法通过默克尔树的校验）。如果该区块仍然链接在原有区块之后，则形成了比主区块链分支更短的新分支，这样的分支将不被大多数节点所认可，成了无效的改动。如果链接在主区块链之后，则该节点必须首先在共识机制下获得记账权，否则其改动也无法被其他节点所认可。

当然，如果某个节点拥有远大于网络中其他节点的算力，在共识机制下总能获得记账权，从而将链接在原区块之后的所有区块都重新链接到篡改后的区块分支中，就能完成区块链的篡改了。但对于大型网络而言，这显然极其困难。

与分布式数据库的区别

上文始终在强调区块链作为一个宏观的数据库而存在，其存储和算力资源来自于世界各地的计算机。而作为当下广泛应用的分布式数据库，似乎也具有相同的特点，其物理存储同样也分布于世界各地的服务器中，该如何区别这两者之间的差异呢？

分布式数据库各节点之间的关系是：信任，协作。

区块链各节点之间的关系是：怀疑，制约。

对于分布式数据库而言，其各存储节点处于同一个信任域，各节点均能独立提供完整的数据库操作，无条件信任另一节点所作的任何修改。因此，从宏观角度来看，它是中心化的，始终由该信任域的所有者控制数据，用户所创造的数据并非由其自己进行控制。

而对于区块链来说，对其他任何节点所做的修改都保持怀疑，不做信任，每一个存储节点都处在不同的信任域中。没有任何独立个体能够随意控制存储在区块链中的数据，换言之，每个用户所创造的数据完全由自己进行控制。因此，区块链是一种去中心化的数据库技术。

实际应用

基于区块链的个人博客 - xLog

个人静态博客从早期的单服务器部署，到如今的 CDN 部署，实际上是在往无服务器模式进行发展的。如果我们的博客文章可以存储在某个巨大的区块链中，不仅能够省去存储资源的花销，还可以使得博客文章不被任何其他审核机制所干预删除。

xLog 就是这样一个开源的基于区块链的个人博客应用，它部署在以太坊区块链上，每一个人都可以使用这个应用创建自己的链上个人博客。当然，由于区块链的特性，所有的编辑操作都将永久地被互联网所记住。

基于区块链的云存储 - IPFS

IPFS 以替代 HTTP 协议成为下一代互联网基石为目标，它将包括 html、js 等在内的网络文件存储在区块链上，而非像如今一样集中存放于中心服务器中，或某家企业的边缘网络服务器上。若中心服务器或 CDN 运营商出现机房故障，则这些文件将无法访问，甚至可能丢失；但在基于区块链的存储方式下，IPFS 协议可以通过在链上查找并从其他各个节点下载获得数据。

结语

互联网领域近年来诞生的新技术、新应用总是朝着建设一个更安全、更自由的网络环境方向发展。然而，去中心化并非总是一个正确的选项，有些应用场景下，我们应当争取一个更加自由的环境，但在另一些场景下，无监管的自由则容易衍生出新的混乱与黑暗。我想这是一个相当深奥的社会学议题，我无法给出一个确切的答案。但就区块链技术本身而言，包括其他追求自由互联网的技术在内，我认为它们是伟大的，其中的技术细节也值得我们进行研究和学习。